第4章 数学基础
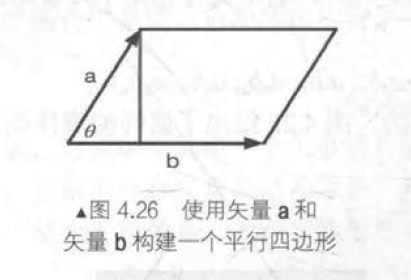
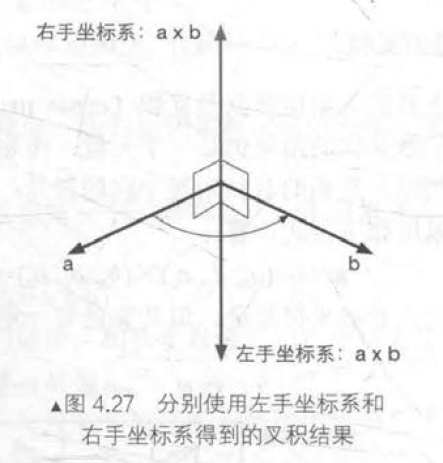
左手坐标系和右手坐标系
在二维笛卡儿坐标系中,我们总可以通过一些旋转操作来使坐标轴指向相同。从这种意义上来说,所有的二维笛卡儿坐标系都是等价的。
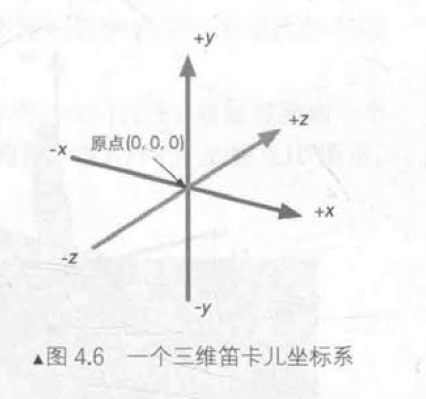
但对于三维笛卡儿坐标系,靠这种旋转有时并不能使两个不同朝向的坐标系重合。因此,就出现了两种不同的三维坐标系:左手坐标系和右手坐标系。
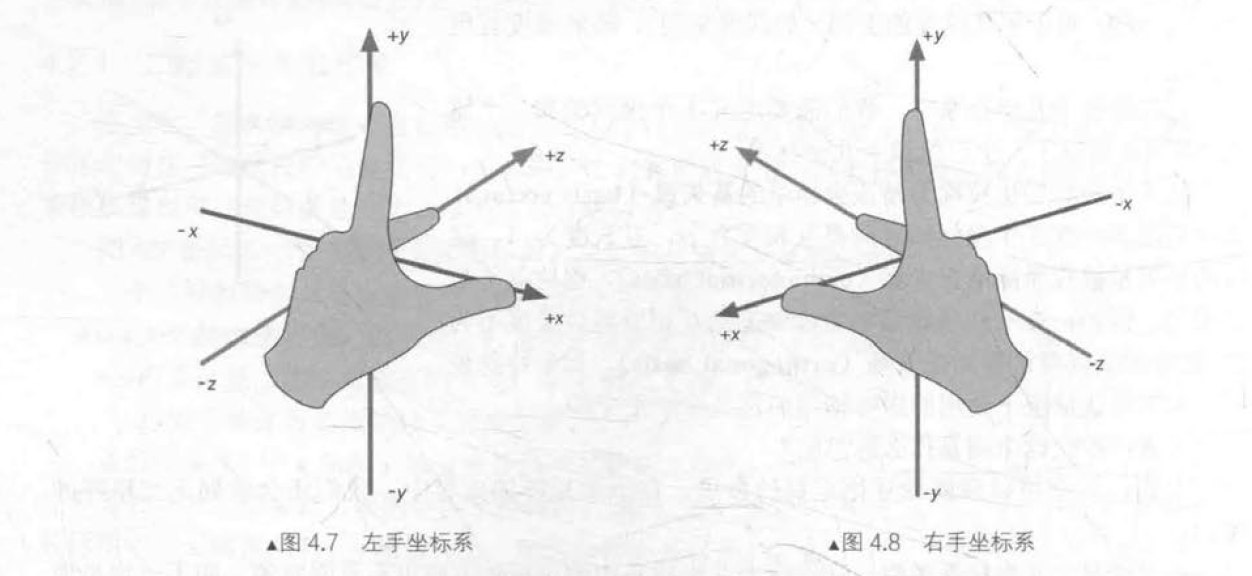
除了坐标轴朝向不同之外,左手坐标系和右手坐标系对于正向旋转的定义也不同,即左手法则(left-band rule)和右手法则(right-band rule)。
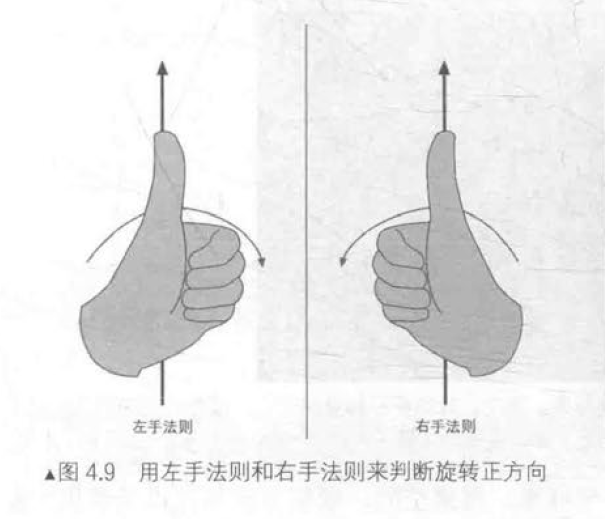
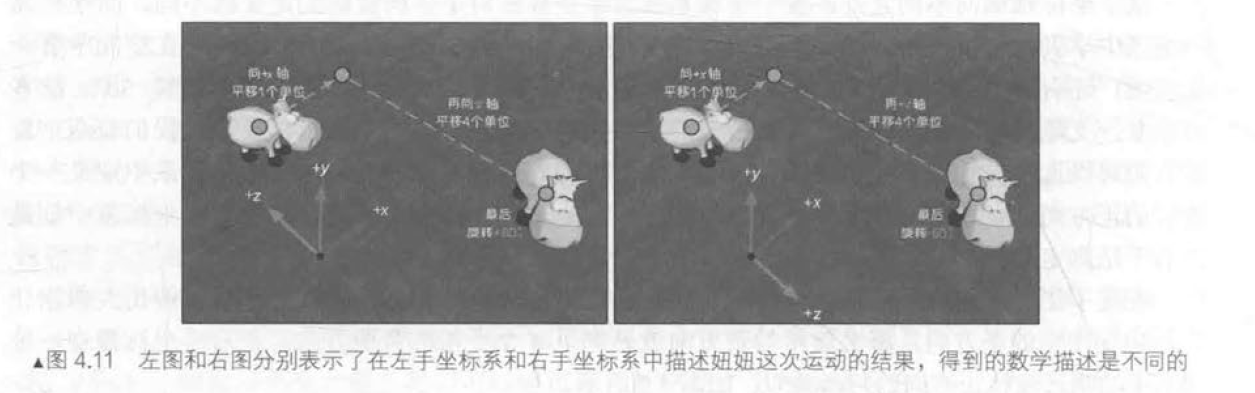
点和矢量
点(point)是n维空间中的一个位置,它没有大小、宽度这类概念。
矢量(vector)是指n维空间中一种包含了模(magnitude)和方向(direction)的有向线段。
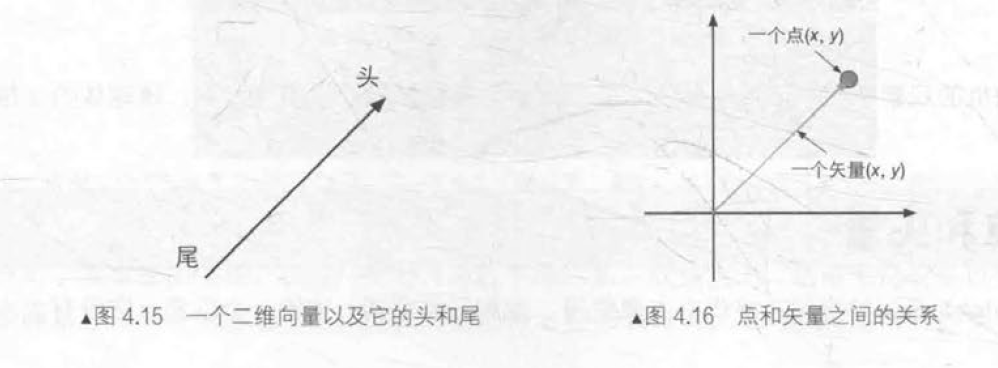
矢量的模
三维矢量的模:\(|v|=\sqrt{v_x^2+v_y^2+v_z^2}\)
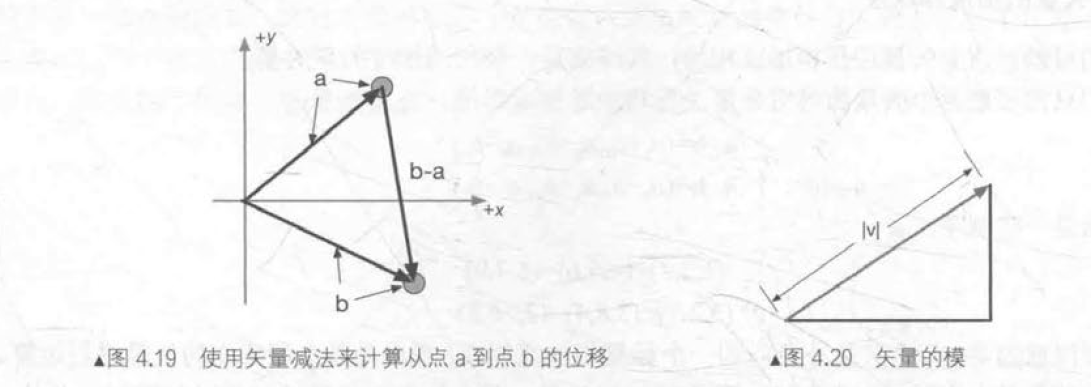
单位矢量
单位矢量指的是那些模为1的矢量,也被称为被归一化的矢量。归一化公式:\(\hat{v} = \frac{v}{|v|}\)
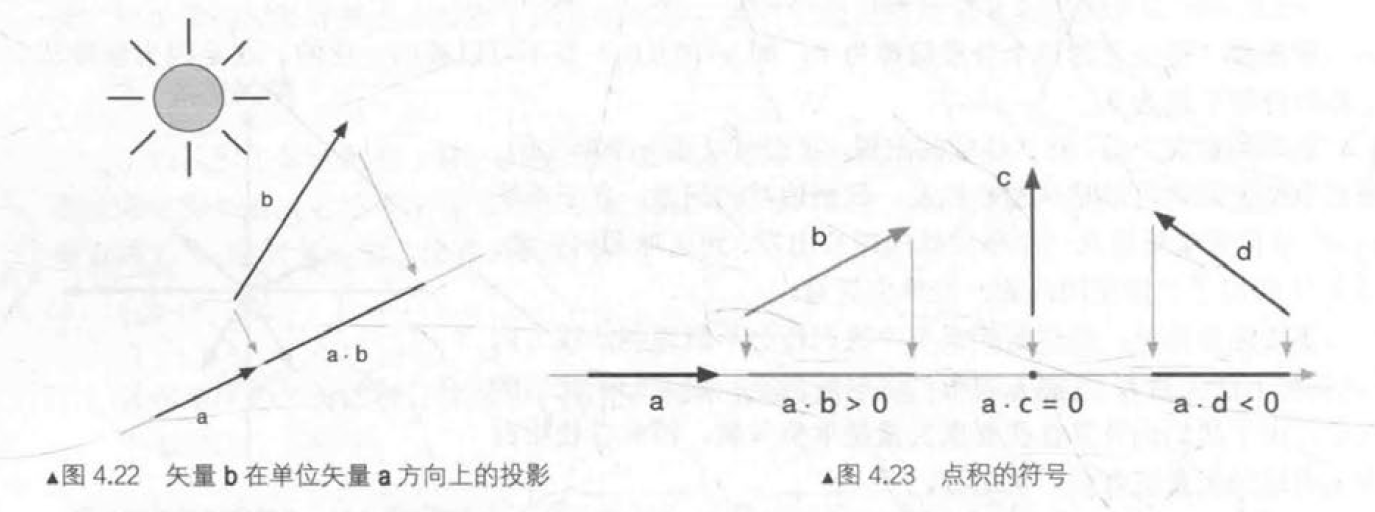
矢量的点积
公式:\(a \cdot b = a_x b_x + a_y b_y + a_z b_z\)

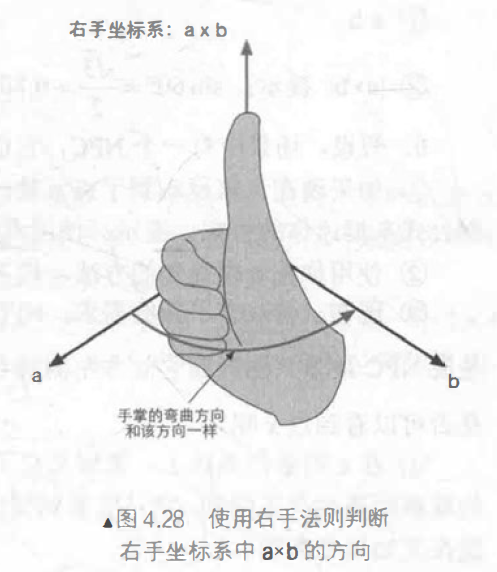
矢量的叉积
叉积的模:\(|a \times b| = |a||b|\sin\theta\)
矩阵
矩阵就是由m×n个标量组成的长方形数组。\(m_{ij}\)表明了这个元素在矩阵m的第i行、第j列。
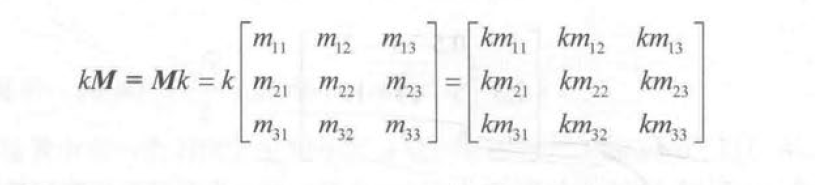

注意:是矢量点乘的结果
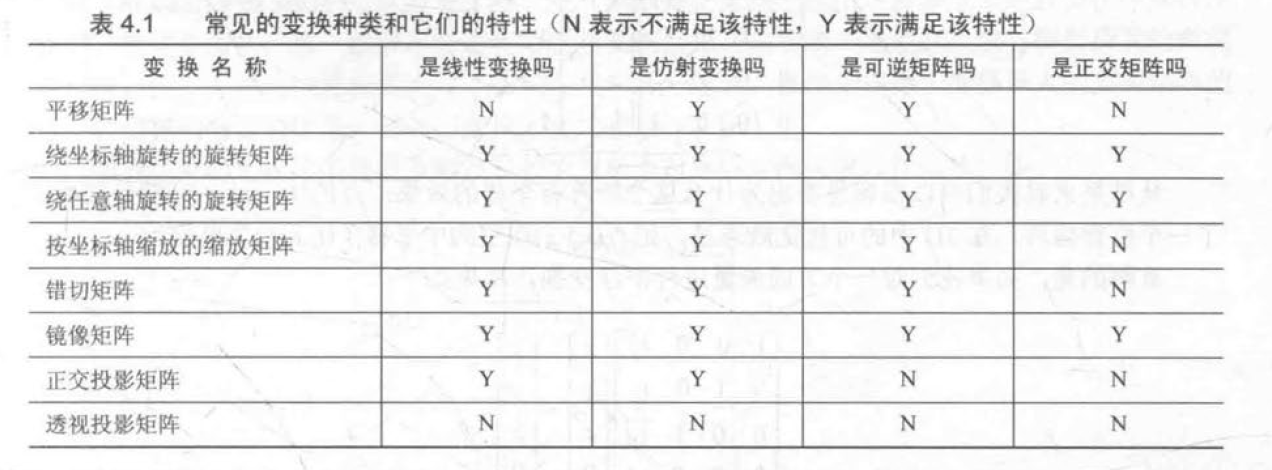
特殊的矩阵





矩阵的几何意义:变换
线性变换与仿射变换
线性变换满足:\(f(x)+f(y)=f(x+y)\) 和 \(kf(x)=f(kx)\)
仿射变换就是合并线性变换和平移变换的变换类型。
齐次坐标
对于一个点,从三维坐标转换成齐次坐标是把其w分量设为1;对于方向矢量,需要把其w分量设为0。
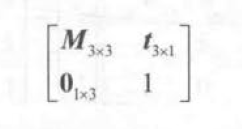
基础变换矩阵
平移矩阵
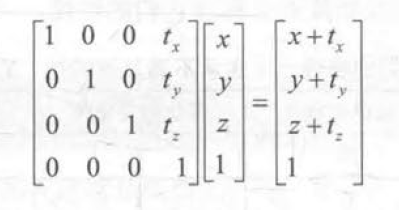
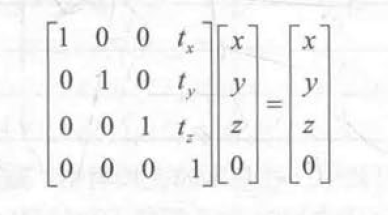
缩放矩阵
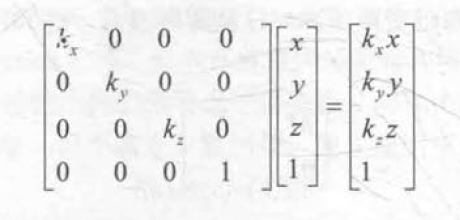
旋转矩阵
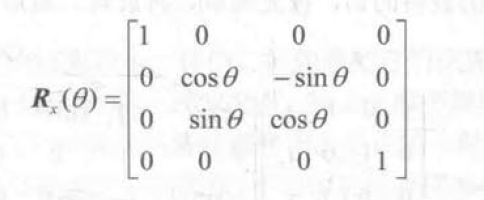
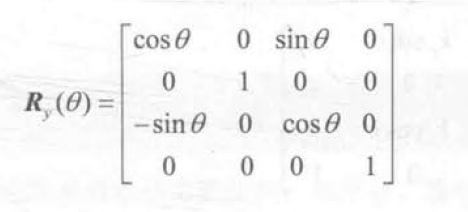

复合变换
在绝大多数情况下,我们约定变换的顺序就是先缩放,再旋转,最后平移。
\(P_{new}=M_{translation}M_{rotation}M_{scale}P_{old}\)

坐标空间
我们需要在不同的情况下使用不同的坐标空间,因为一些概念只有在特定的坐标空间下才有意义。

坐标空间的变换
\(A_p=M_{c→p}A_c\) 和 \(B_c=M_{p→c}B_p\)


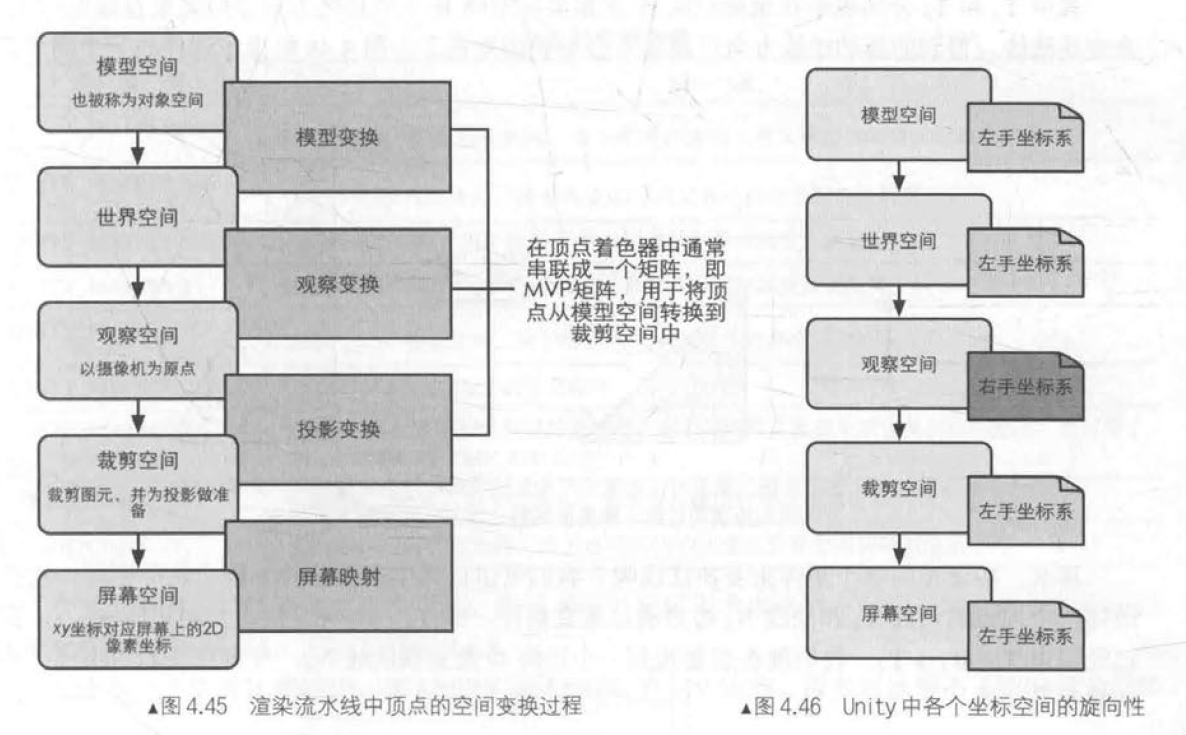
顶点的坐标空间变换过程
一个顶点最开始是在模型空间中定义的,最后它将会变换到屏幕空间中。
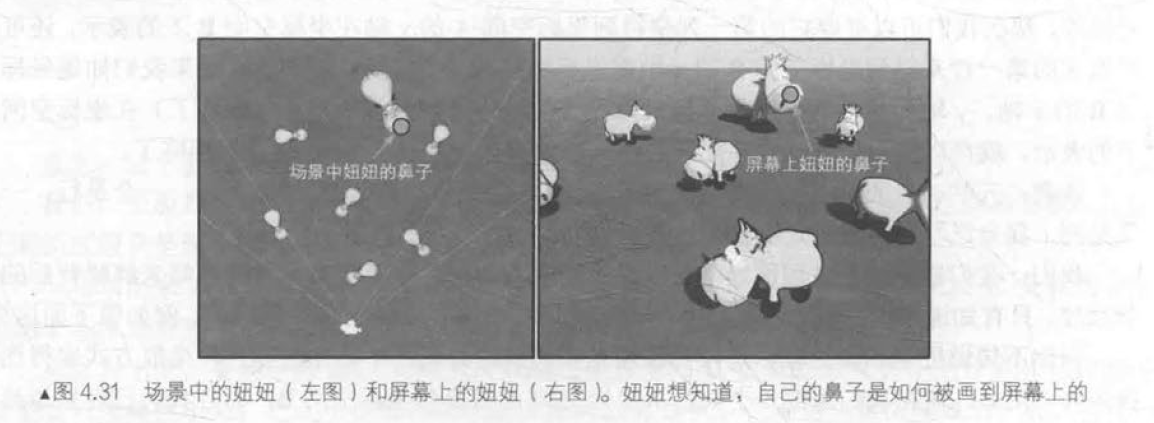
模型空间
Unity在模型空间中使用的是左手坐标系,+x轴、+y轴、+z轴分别对应的是模型的右、上和前向。
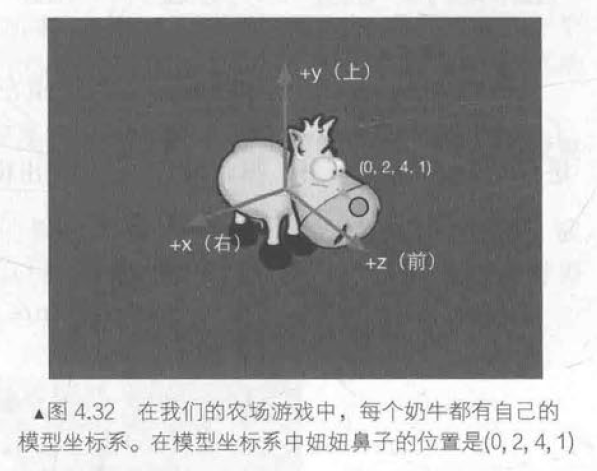
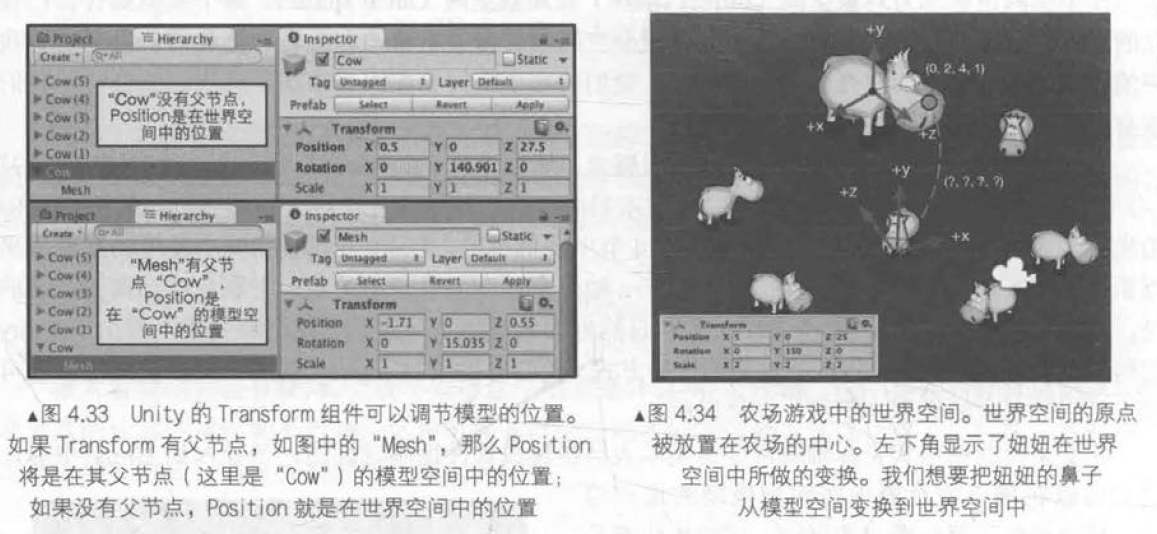
世界空间
顶点变换的第一步,就是将顶点坐标从模型空间变换到世界空间中。这个变换通常叫做模型变换(model transform)。
观察空间
Unity中观察空间使用的是右手坐标系:+x轴指向右方,+y轴指向上方,而+z轴指向的是摄像机的后方。


裁剪空间
裁剪空间的目标是能够方便地对渲染图元进行裁剪。

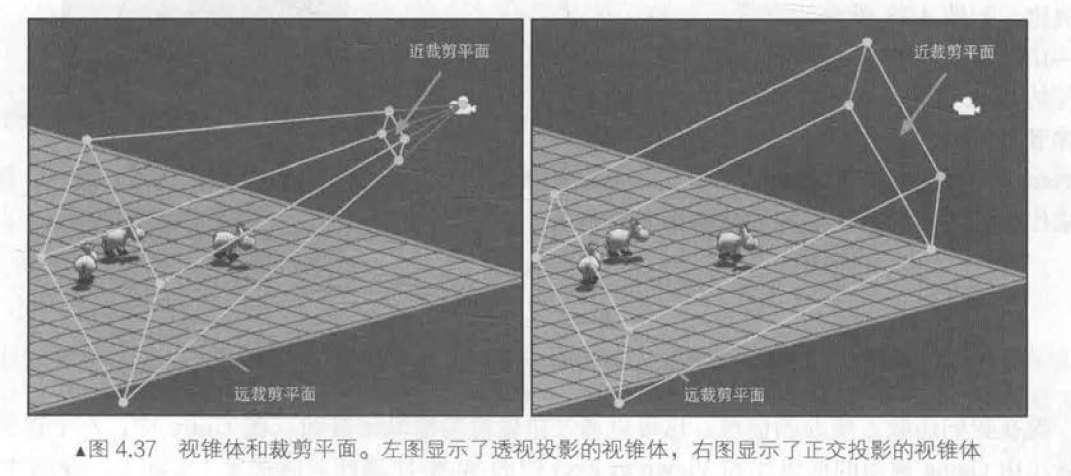
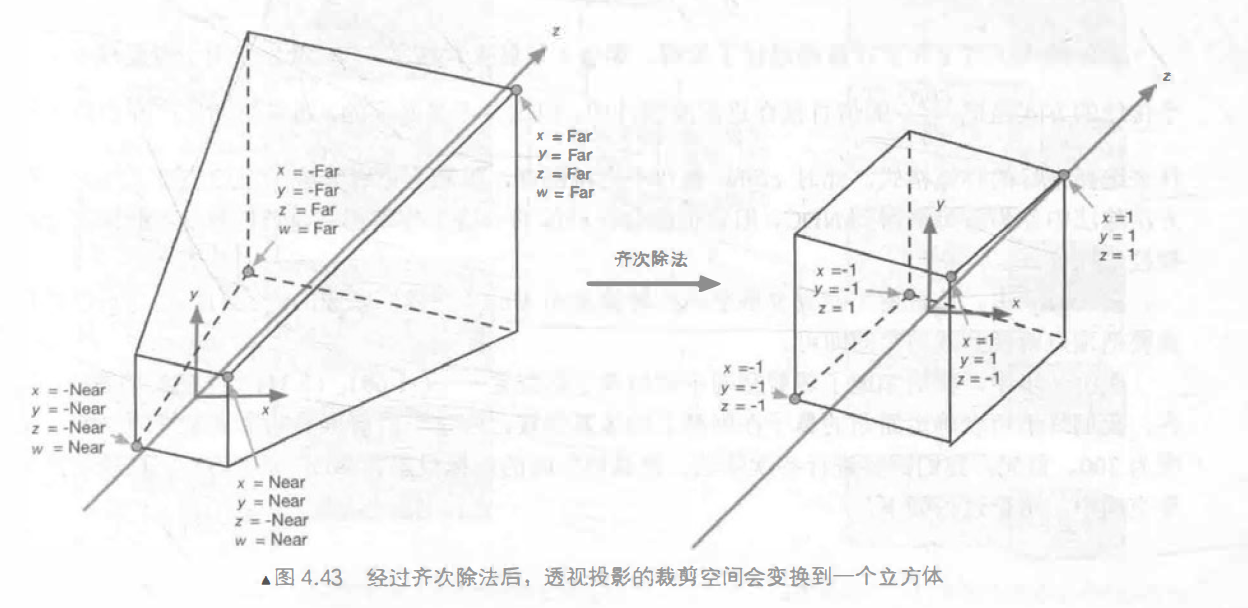
透视投影:
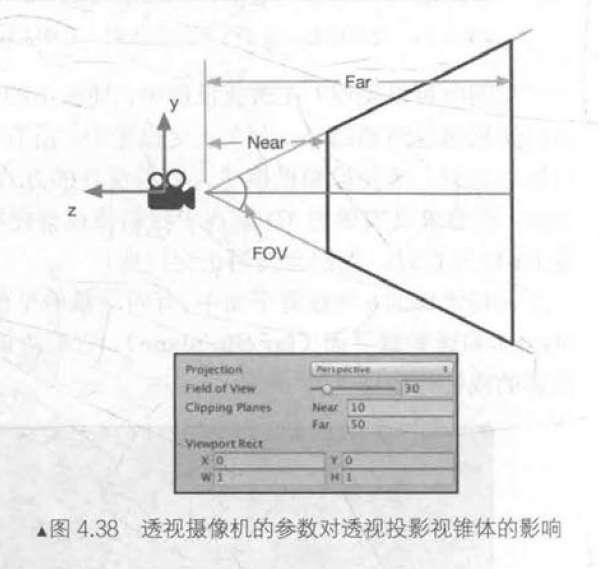
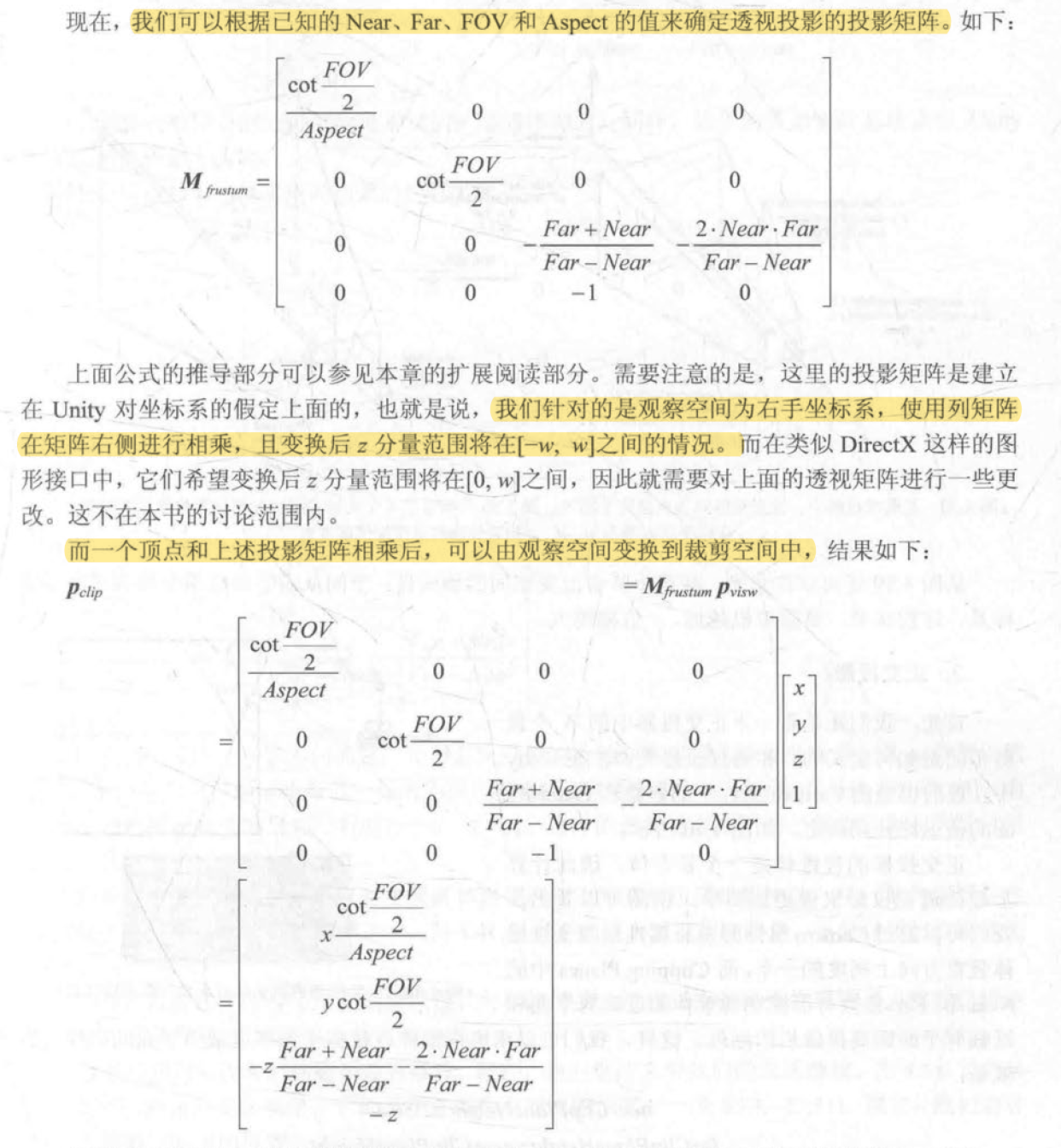
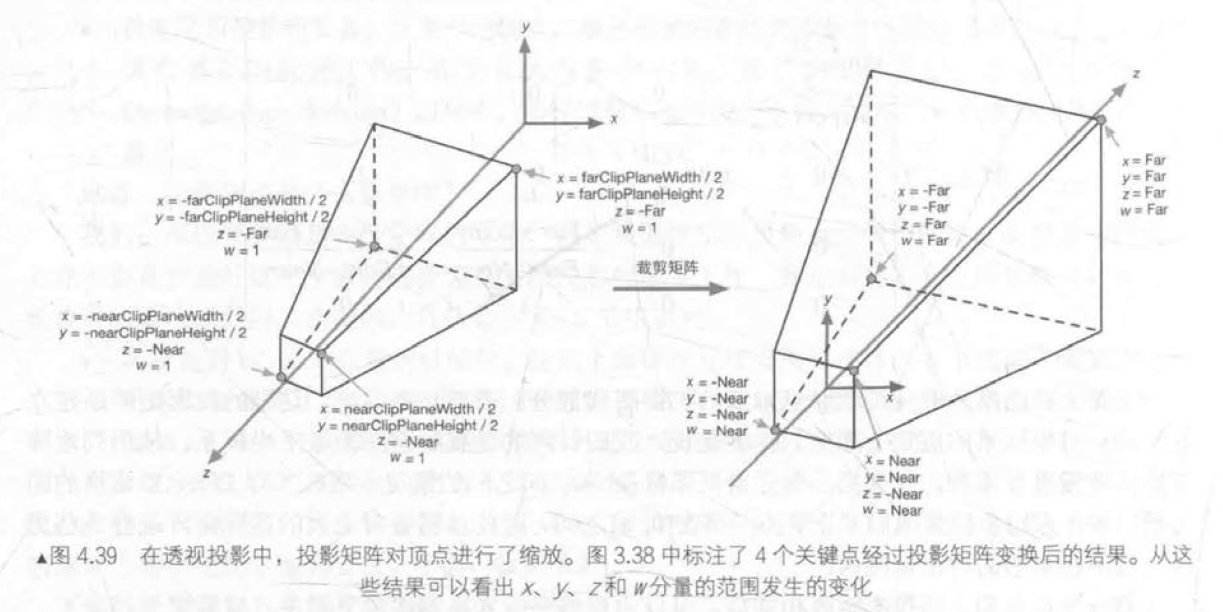
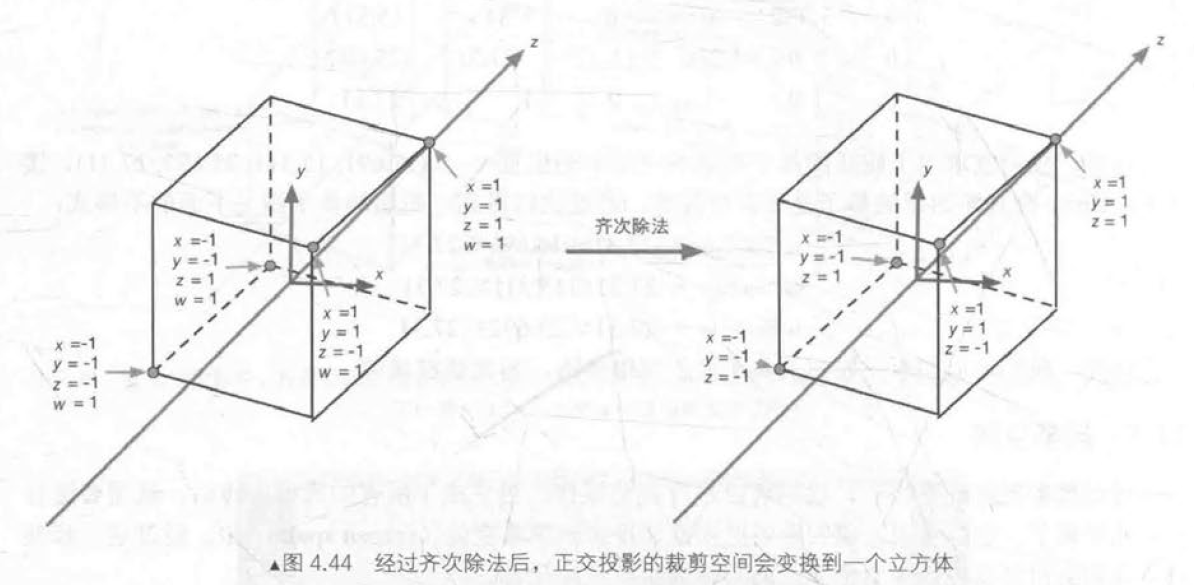
正交投影:
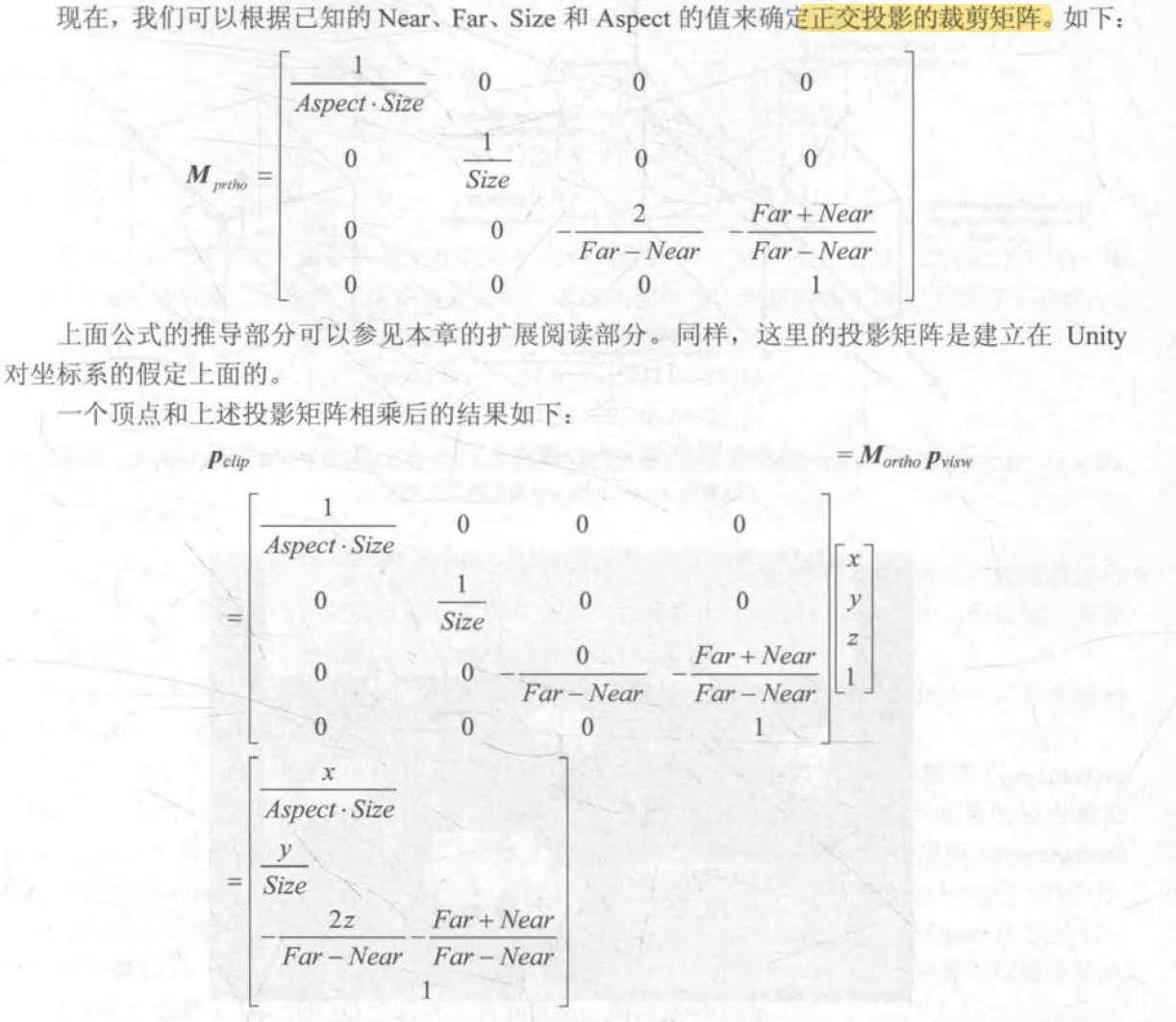
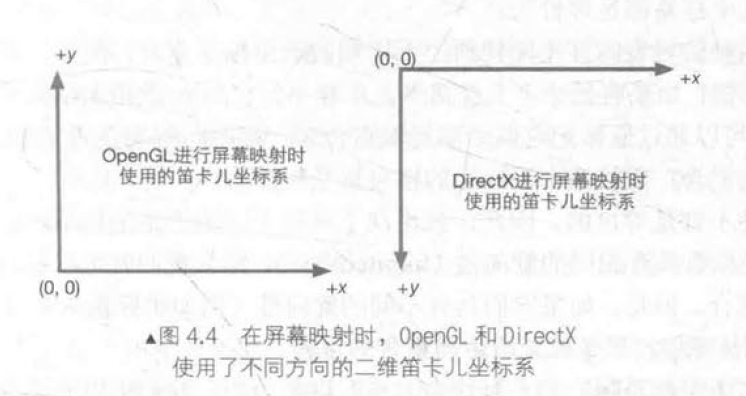
屏幕空间
经过投影矩阵的变换后,我们可以进行裁剪操作。完成裁剪后需要进行真正的投影,把视锥体投影到屏幕空间中。

总结